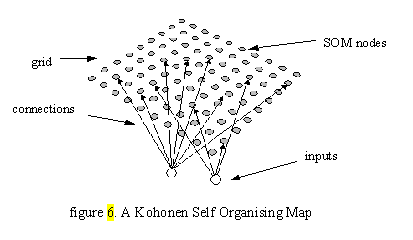
What the SOM aims to do is to group together training patterns exhibiting similar traits into 'clusters'. These clusters, represented by groups of nodes in the map, can then be labelled by the user and used to identify further patterns.
Training and identification is carried out by letting nodes in the map 'compete' with each other when presented an input pattern.
The structure of the SOM can be seen in figure 6. Nodes are organised into a two dimensional grid, each node in the grid being connected with each input node.

During each epoch of the training cycle, all patterns of the training set are presented to the map. A winning node is chosen for each pattern, and is decided as the node whose weight vector most closely matches that of the input vector. This node can be found using the following equation (Kohonen 1998):

  where x_i(t) is the i^th input at time t
  w_ji(t) is the weight between input i and node j
  n is the total number of nodes.

The winning node will be the node with the minimum value of d_j. The weights of that node are then adjusted to more closely match that of the input vector, using the following equation (Kohonen 1998):

  where w_j is the weight vector of node j at time t
x(t) is the input vector at time t
h_j,k(t) is the neighbourhood function between nodes j and k (see below)
h(t) is the learning rate at time t given by the equation (Haykin, 1999):

here, h₀ is the initial learning rate. The time constant t₁ controls the rate at which h falls.