A recursive function is one that calls itself. We will begin by looking at the calculation of a factorial.
Factorials are often used in statistical calculations. The factorial of n, written as n! is equal to the product of n(n-1)(n-2)...(1). For example 4! is equal to 4 × 3 × 2 × 1 = 24. There is an obvious way to do this calculation using a loop, but we can also do it recursively.
Let's consider the definition of a factorial in a slightly different way:
Let's look at an implementation of our recursive factorial function.
int fact(int n)
{ if (n == 0) return 1;
else return n * fact(n - 1);
}
There are some key properties that all recursive functions exhibit:
This function takes a series of characters and outputs them in reverse order.
#include <iostream>
using namespace std;
void rev( )
{ char ch;
cin.get(ch);
if (ch != '\n')
{ rev();
cout.put(ch);
}
}
int main( )
{ rev();
}
Assume that the input is a single line of characters
ABCD
The first call to rev reads the letter A (so we are now positioned between A and B in the input stream), decides it is not the newline
character, and calls rev. It then waits until this call to rev has completed.
The second call to rev begins by reading a letter; this time it's B.
The first call and the second call are separate calls, so each one has its
own local variable ch. So the first call is holding A in its local ch, and the
second call is holding B in its local ch. (Think of them as separate people
following the same instructions rather than as one person.) The second call
decides that its char is not the newline character and it calls rev. The
second call now waits until the third call has finished.
You can picture successive calls like this:
When we get to call number 5, the recursion bottoms out because the character
read by call 5 is the newline character, so it does not make a call to rev;
in fact it does nothing at all except terminate, i.e. return.
Call 4 then wakes up and carries on from where it left off, i.e. it goes on
to do its cout.put(ch); Its char is D so we get a D in the output. It then finishes. Call 3, which has been waiting for call 4 to finish, now wakes up and outputs its character, which is C, so the next thing we get in the output is a C. And so on. The eventual output is
DCBA
The next examples are just for illustration - you would probably not choose to use recursion for these. Later we will see examples where recursion, if not the only way to do it, is easily the best.
This function takes as its arguments a vector<int> and the index of the last element it needs to bother with. A typical function call will be: total = sum(v, static_cast<int>(v.size()) - 1);
int sum(const vector<int>& v, int top)
{ if (top < 0) return 0; // empty vector
else return v[top] + sum(v, top - 1);
}
bool anyneg(const vector<int>& v, int top)
{ if (top < 0) return false; // no negatives in empty vector
else return v[top] < 0 or anyneg(v, top - 1);
}
bool there (const vector<int>& v, int top, int val)
{ if (top < 0) return false;
else return v[top] == val or there(v, top - 1, val);
}
A palindrome vector would be one where one half was a mirror-image of the other, such as 7 6 9 6 7 or -5 66 66 -5. We will say that a vector of zero elements or of just one element is a palindrome.
The algorithm starts from the extreme ends of the vector and terminates when
it reaches the middle of the vector (the high and low
indexes pass one another). The call might be mirror(v, 0, static_cast
bool mirror (const vector<int>& v, int low, int high)
{ if (high <= low) return true;
else return v[low] == v[high] and mirror(v, low + 1, high - 1);
}
Rather than using two indexes, this algorithm returns the inner substring, minus its first and last elements, until the string is of length one or less.
bool mirror(string s)
{ if (s.length() <= 1) return true;
return s[0] == s[s.length() - 1]
and mirror(s.substr(1, s.length() - 2);
}
Note that in this example I haven't bothered to use an else.
(I didn't actually need one in the other examples either.) The reason we can do without one here is that a return terminates the function immediately. So, if the bottoming-out condition is true and the first return is executed, the second return will not be reached.
The beauty of recursive programming is that the functions tend to be very small and elegant. The looping is taken care of by the recursion, rather than the programmer having to write the loop explicitly.
int sumlist(Node* head)
{ if (head == NULL) return 0; // empty list
else return head->val + sumlist (head->link);
}
int no_nodes (Node* head)
{ if (head == NULL) return 0;
return 1 + no_nodes (h->link);
}
void print_num(Node* head)
{ if (head != NULL)
{ cout << h->n << " ";
print_num(head->link);
}
}
Note that a procedure, unlike a function, does not have to do anything.
(A function must always return a value.) So if, as here, we do not want to
do anything for an empty list, it is neater to state the condition as if (head != NULL) rather than if (head == NULL)
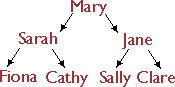
Consider the way some groups of people organise themselves to make sure that everyone in the group is informed while sharing the burden of the phone bill. Each person only has to phone two others, and the news eventually filters down to everyone.
 |
This works fine when the information is only travelling in one direction, but what happens when we need to find something out from someone in the group. Imagine Mary needed to get hold of a book. She could just put out a general call to everyone, but then she might end up with three copies of the book at the next meeting, or none. It would be better to have a way to ask each person in turn, then when she got through the whole group she would be sure of having only one copy of the book, or none.
The algorithm Mary would use in this case would be:
When Mary rings Sarah, Sarah will use the same algorithm herself, checking her bookshelf, then ringing Fiona and Cathy before getting back to Mary to say whether anyone on her branch has a copy. In a sense, Fiona and Cathy also use the same algorithm except that, since they have no-one to ring, they can skip lines 2 and 3.
If we adapt this analogy to a binary tree of Binodes, e.g.
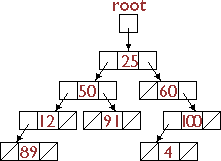 |
we can use a function call of the form if (there(root, 91)) ... to search the tree to see if it contains the value 91.
bool there(Binode* troot, int x)
{ if (troot->n == x) return true; // Mary has a copy
if (troot->l != NULL and there(troot->l, x)) return true; // Someone down Sarah's side has a copy
if (troot->r != NULL and there(troot->r, x)) return true; // Someone down Jane's side has a copy
return false; // No-one has a copy
}
This is fairly straightforward code, but it is weak on two counts:
Let's deal with the NULL pointer problem - here, as often, getting that right actually simplifies the rest:
bool there (Binode* troot, int x)
{ if (troot == NULL) return false;
return (troot->n == x) or there(troot->l, x) or there(troot->r, x);
}
Remember that booleans are evaluated left to right and a value is returned as early as possible. If (troot->n == x) is true, then (there(troot->l, x)) and (there(troot->r, x)) are not evaluated. (If Mary has the book, she won't bother Sarah or Jane.) If (troot->n != x) , then (there(troot->l, x)) is evaluated; if it comes back with true, then (there(troot->r, x)) is not evaluated. (If Mary does not have the book but Sarah comes back with a Yes, she won't bother Jane.)
Notes on R. Mitton's lectures by S.P. Connolly, edited by R. Mitton, 2000