What's wrong with this picture?

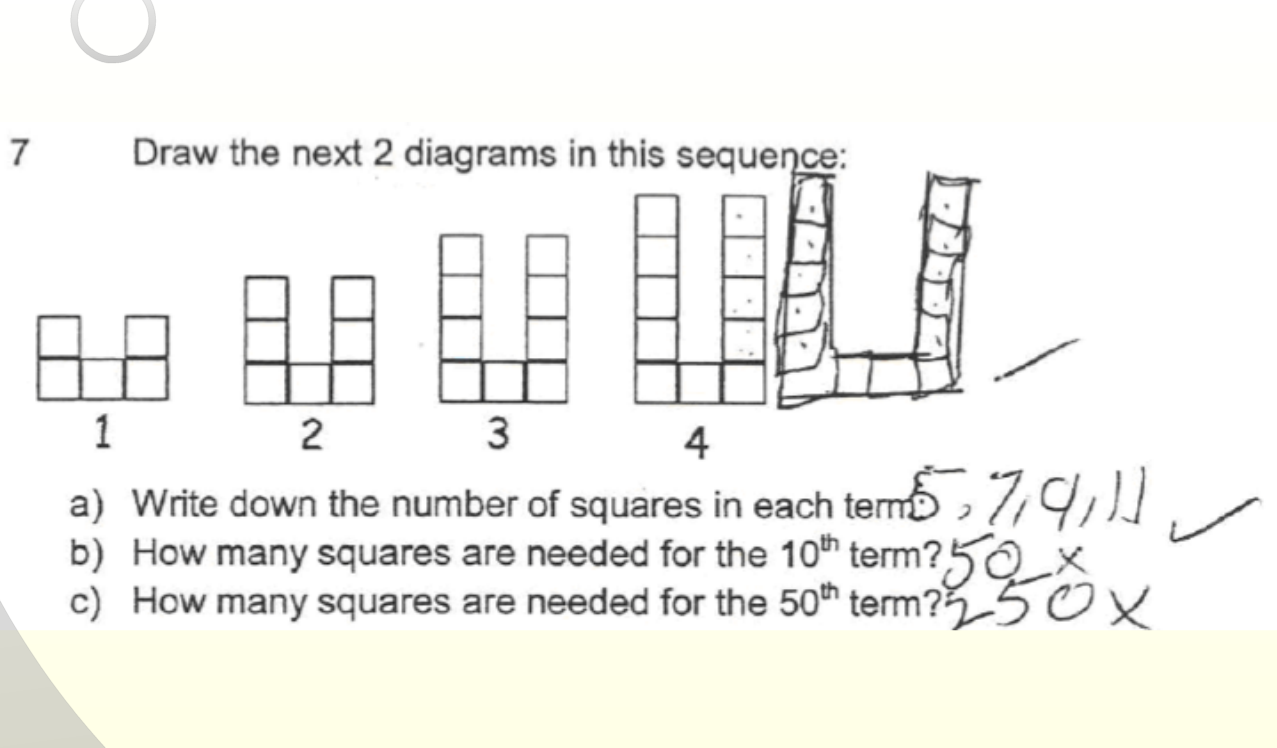
If you ask kids to predict the number of tiles in a pattern like this, they'll count. And why shouldn't they, given the question? So here, a student has counted the number of tiles: 5, 7, 9, 11. And then says, 'How many squares are needed for the tenth term? Well, it must be 10 times 5.' Which is wrong. And how many squares are needed for the 50th term? 'It must be 5 times 50.' Which is also wrong.

The problem is that teachers in the current curriculum are encouraged to foster a way of thinking amongst the kids in which they break, as soon as possible, the reference to what they're thinking about. So the teacher says, 'Don't think about tiles; write down the sequence then guess the next number.' And so, mathematics becomes a pattern-spotting activity, instead of a way of linking generalisations to the structure of the phenomenon you're looking at.

This is a really big problem. Mathematics education researchers have been worried about it for more than 20 years. It also stands in the way of children understanding what these letters are:

And thus, if you ask anybody who felt bad about their secondary maths education, and ask 'At what point did it become untenable for you?' they'll say, 'When the teacher wrote down "n".'

It doesn't help when teachers say things like, 'Make your rule true for any value.' Because then the teacher is thinking, 'any value of an infinite number, and it has to be true for them all at once.' The kid is simply thinking, 'any value.' For example, '17.' So there is a mismatch between the teacher's thinking and the student's thinking.

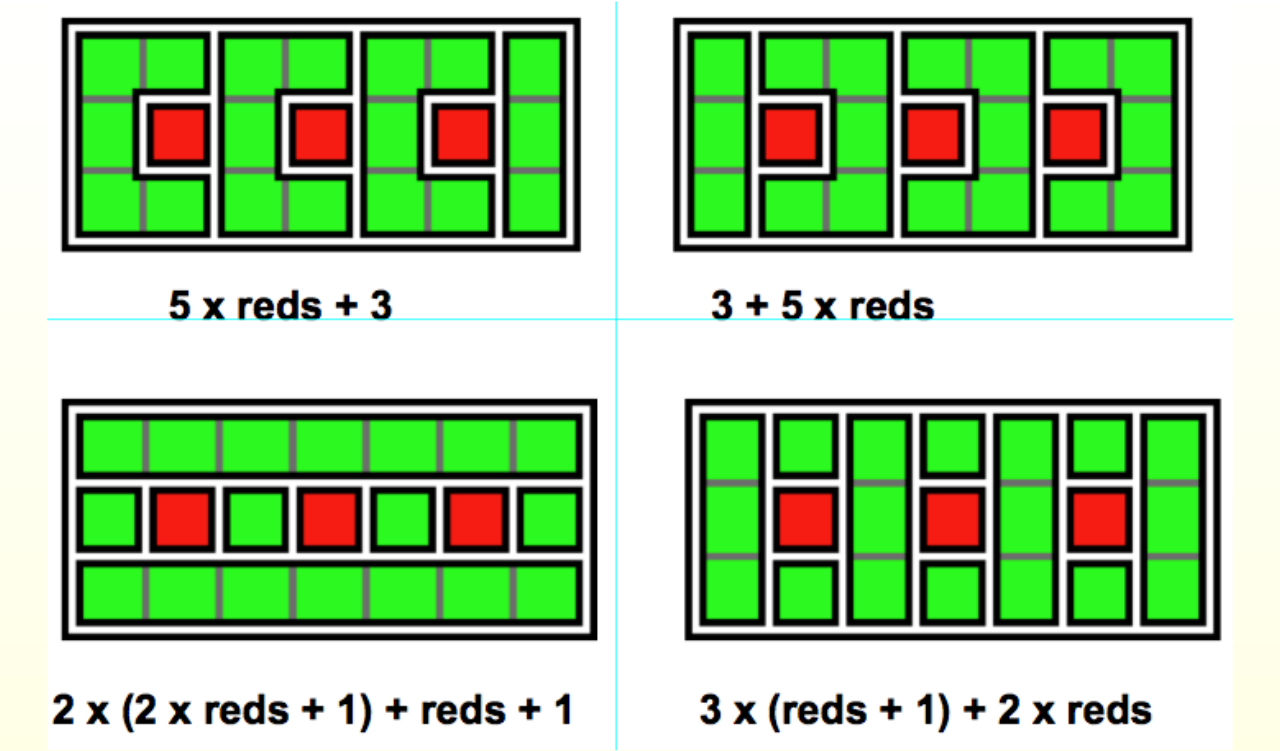
One way that we've found very productive is to try and find a system in which the logic of failing to generalise - of making something true for every case - results in some visual image being 'messed up,' some structure disappearing.

The trick is, you've got to try to give kids the experience that mathematicians find routine. Which is: Do specific things, while keeping part of your attention on what would happen in the general case. It's fantastically difficult, and it's the essence of what mathematics is, and it doesn't really happen in any other walk of life.

So the first element of the system we've built is about construction, and you can see above different ways of constructing a footpath. Here, a green path with, say, little red flower pots. The question is, How can you describe that pattern?

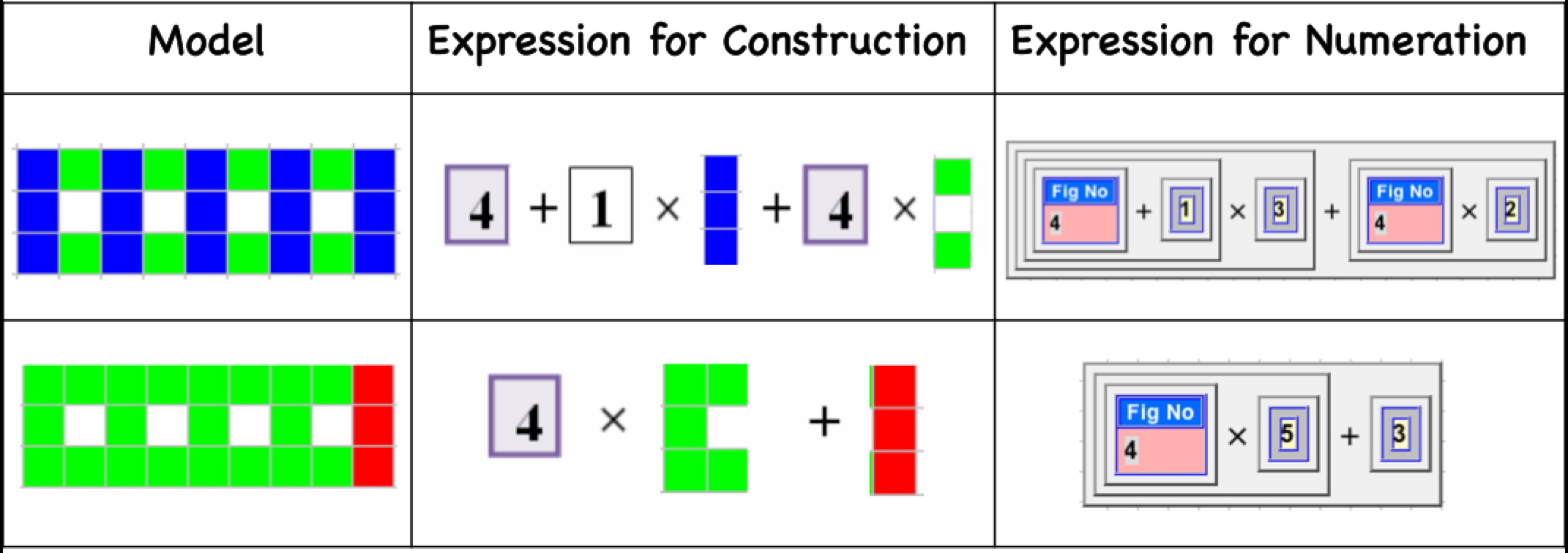
MiGen provides an intermediate language that is a pathway to formal algebra. Starting from your construction, you can develop an expression for it, and then the system helps you build an expression for numeration.

In the second case in the above table, for example, the structure is expressed as '4 times the green "C" plus the red column.' And the system provides a language for this to be translated into an expression for numeration, like the one shown above, which is quite similar to an actual algebraic expression.

The 'generality' of the expression is made possible by the 'unlocked' number, ('Fig No.' in this example). This means that the student (or the system itself) can assign any value to it.

To help students develop this intermediate language leading to algebra, the system is designed to provide help through prompts that appear when a Help Box is clicked, or when a Help Question is selected. The help is personalised - adapted to the student's work so far.

You can try it for yourself.